Introduction:
In the realm of statistical hypothesis testing, researchers frequently encounter two fundamental types of errors: Type 1 and Type 2. These errors, also known as false positives and false negatives, respectively, can significantly impact the validity and reliability of research findings across various disciplines. As a researcher, understanding these concepts is crucial for conducting robust studies and drawing accurate conclusions from your data. This comprehensive guide will delve deep into the nature of Type 1 and Type 2 errors, their implications for research, and strategies to minimize their occurrence.

1. Understanding Type 1 and Type 2 Errors
1.1 Type 1 Error (False Positive) Definition: A Type 1 error occurs when we reject the null hypothesis when it is actually true. In simpler terms, it's concluded that there is a significant effect or difference when, in reality, there isn't one.
Example: Imagine a pharmaceutical company is testing a new drug for lowering blood pressure. The null hypothesis is that the drug has no effect. If the researchers conclude that the drug is effective when it actually isn't, they've committed a Type 1 error.
Implications: Type 1 errors can lead to:
-
Unnecessary interventions or treatments
-
Wasted resources on ineffective solutions
-
Potential harm to subjects or patients
-
Misleading scientific literature and public knowledge
1.2 Type 2 Error (False Negative) Definition: A Type 2 error occurs when we fail to reject the null hypothesis when it is actually false. In other words, it's concluding that there is no significant effect or difference when, in reality, there is one.
Example: Using the same pharmaceutical scenario, if the researchers conclude that the blood pressure drug is ineffective when it actually does work, they've committed a Type 2 error.
Implications: Type 2 errors can result in:
-
Missed opportunities for beneficial interventions
-
Overlooking important effects or relationships
-
Potentially delaying scientific progress
-
Underestimating the impact of variables or treatments

2. The Relationship Between Type 1 and Type 2 Errors
It's important to note that Type 1 and Type 2 errors are inversely related. As you decrease the probability of one type of error, you generally increase the probability of the other. This relationship creates a challenge for researchers in balancing the two risks.
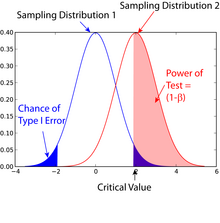
Key concepts in this relationship:
-
Significance level (α): The probability of committing a Type 1 error
-
Power (1 - β): The probability of correctly rejecting a false null hypothesis
-
β: The probability of committing a Type 2 error
The trade-off: Lowering the significance level (α) to reduce Type 1 errors will increase the likelihood of Type 2 errors, and vice versa. This balance is a crucial consideration in research design.
3. Factors Influencing Type 1 and Type 2 Errors
Several factors can affect the likelihood of committing these errors:
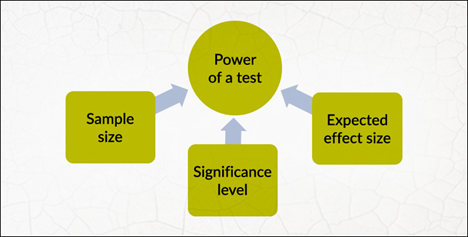
3.1 Sample Size:
-
Larger sample sizes generally reduce both types of errors
-
Smaller samples are more prone to both Type 1 and Type 2 errors
3.2 Effect Size:
-
Larger effect sizes are easier to detect, reducing Type 2 errors
-
Smaller effect sizes require larger samples to maintain power
3.3 Variability in the Data:
-
Higher variability increases the chance of both error types
-
More homogeneous data can help reduce error rates
3.4 Chosen Significance Level:
-
A stricter significance level (e.g., 0.01 instead of 0.05) reduces Type 1 errors but may increase Type 2 errors
3.5 Study Design:
-
Well-designed studies with appropriate controls and randomization can help minimize both types of errors
4. Strategies to Minimize Type 1 and Type 2 Errors
4.1 Adjusting Significance Level (α):
-
Traditionally, researchers use α = 0.05 or 0.01
-
For critical decisions or high-stakes research, a lower α may be appropriate
-
Consider the context and potential consequences when setting α
4.2 Increasing Sample Size:
-
Larger samples provide more statistical power
-
Use power analysis to determine the optimal sample size
-
Be mindful of diminishing returns and practical constraints
4.3 Improving Study Design:
-
Use appropriate control groups
-
Implement randomization techniques
-
Control for confounding variables
-
Ensure proper measurement techniques and instruments
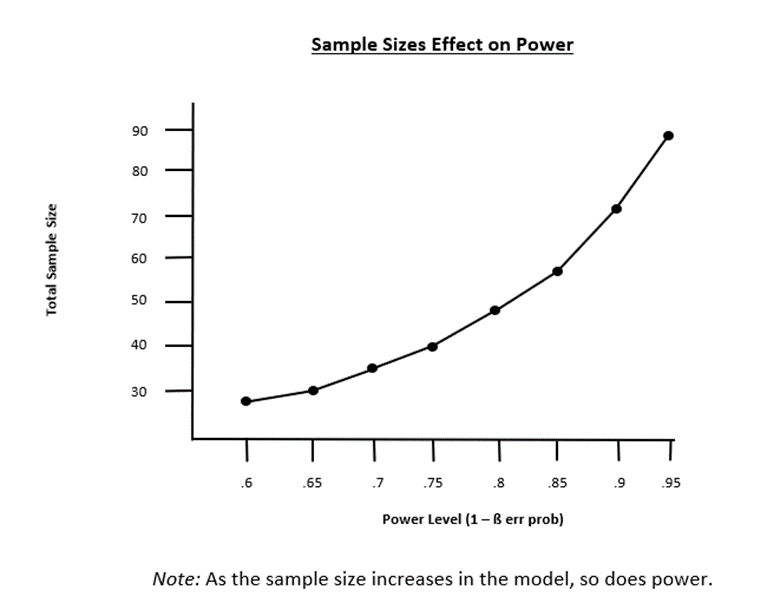
4.4 Conducting Power Analysis:
-
Perform a priori power analysis to determine required sample size
-
Aim for a power of 0.8 or higher to reduce Type 2 errors
-
Consider effect size, significance level, and desired power in calculations
4.5 Considering Effect Size:
-
Focus on practical significance, not just statistical significance
-
Use standardized effect size measures (e.g., Cohen's d, r, η²)
-
Interpret results in the context of your field and research question
4.6 Implementing Multiple Testing Correction:
-
When conducting multiple hypothesis tests, use correction methods
-
Examples include Bonferroni correction, False Discovery Rate (FDR) control
-
These methods help maintain the overall Type 1 error rate at the desired level
4.7 Replication and Meta-Analysis:
-
Reproduce studies to validate findings
-
Conduct meta-analyses to synthesize results from multiple studies
-
This approach helps to establish the robustness of effects and reduce error rates
4.8 Using Bayesian Approaches:
-
Consider Bayesian statistics as an alternative to frequentist hypothesis testing
-
Bayesian methods can provide more nuanced interpretations of evidence
-
They allow for updating beliefs based on prior knowledge and new data
5. Real-World Examples and Case Studies
5.1 Medical Research: In drug trials, Type 1 errors could lead to approving ineffective or potentially harmful medications. Type 2 errors might result in overlooking effective treatments. The FDA typically requires multiple large-scale trials and stringent significance levels to minimize these risks.
Case Study: The development and testing of COVID-19 vaccines in 2020 highlighted the importance of balancing speed with rigorous testing to avoid both types of errors.
6. Advanced Considerations
6.1 Machine Learning and Big Data:
-
In big data analyses, the risk of Type 1 errors increases due to multiple testing
-
Techniques like cross-validation and regularization help mitigate these risks
-
The concept of overfitting in machine learning is related to Type 1 errors
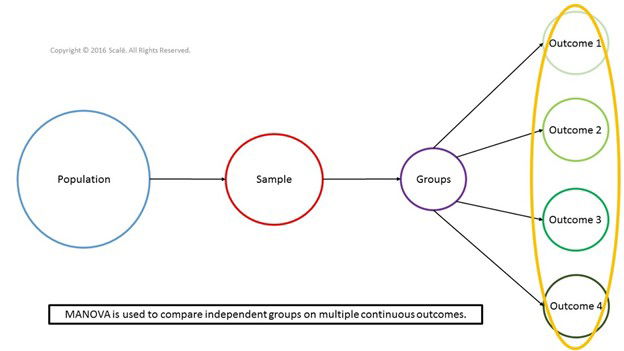
6.2 Multivariate Analyses:
-
When dealing with multiple variables, the complexity of error control increases
-
Methods like MANOVA and discriminant analysis require careful consideration of both error types
6.3 Longitudinal Studies:
-
Time-series data present unique challenges in error control
-
Autocorrelation and time-dependent effects must be considered
6.4 Qualitative Research:
-
While not directly applicable, the concepts of Type 1 and Type 2 errors can inform qualitative research design
-
Triangulation and member checking can serve similar roles in enhancing validity
7. Ethical Considerations
When designing studies and interpreting results, researchers must consider the ethical implications of both types of errors:
-
Type 1 errors in medical research could lead to unnecessary treatments or interventions
-
Type 2 errors might result in withholding potentially beneficial treatments
-
Balancing these risks requires careful consideration of potential harms and benefits
-
Transparency in reporting methods, results, and limitations is crucial
8. Future Directions and Emerging Approaches
8.1 Adaptive Design:
-
Sequential analysis and adaptive trial designs allow for ongoing assessment and adjustment
-
These approaches can help optimize resource use and potentially reduce both types of errors
8.2 Preregistration and Registered Reports:
-
Preregistering study designs and analyses can help reduce researcher degrees of freedom
-
This approach addresses issues related to p-hacking and publication bias
8.3 Open Science and Data Sharing:
-
Increased transparency and data availability allow for better error detection and correction
-
Collaborative efforts can lead to larger samples and more robust findings
Conclusion:
Understanding and addressing Type 1 and Type 2 sampling errors is fundamental to conducting rigorous and reliable research. As a postgraduate researcher, your awareness of these concepts will enhance the quality of your work and contribute to the advancement of your field. By implementing the strategies discussed in this guide, you can minimize the occurrence of these errors and increase the validity of your findings.
Remember that the goal is not to eliminate these errors entirely, as that is impossible, but to strike an appropriate balance based on the context of your research. Continual learning, critical thinking, and adherence to best practices in research methodology will serve you well in navigating the complexities of Type 1 and Type 2 errors throughout your academic and professional career.


